SUMPRODUCT 함수로 조건을 만족하는 자료만 계산하기

엑셀의 SUMPRODUCT 함수는 주어진 인수를 모두 곱한 후에 합계를 구해줍니다.

SUMPRODUCT 함수 기본 사용법은 다음 글을 참고하세요.
[ SUMPRODUCT 함수 - 숫자를 모두 곱하고 합계 구하기 ]

단순히 곱해서 합계를 구하는 기능을 넘어서 좀 더 응용하면 특정 조건을 만족하는 행만 곱하고 곱한 자료만 따로 계산할 수 있습니다. 이 기능이야말로 SUMPRODUCT 함수의 진정한 가치라고 할 수 있습니다.

이 예는 구조가 약간 복잡해서 이해하기 쉽지 않지만 실무에서 많이 사용되므로 잘 익혀 두면 조건 별로 처리를 해야 할 때 아주 요긴하게 사용할 수 있습니다.

실습용 엑셀파일 다운로드 : 엑셀-SUMPRODUCT-함수로-조건을-만족하는-자료의-합계구하기.xlsx

수식 입력

아래의 표에서

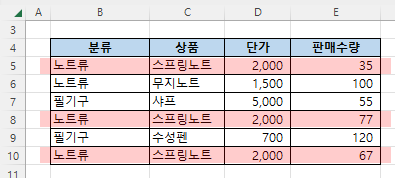
분류가 "노트류"이고
상품명이 "스프링노트"인

것의 판매금액(단가 x 판매수량) 합계를 구해보겠습니다.

[C32] 셀에 다음 수식을 입력합니다.
=SUMPRODUCT((B5:B10="노트류")*(C5:C10="스프링노트"),D5:D10,E5:E10)

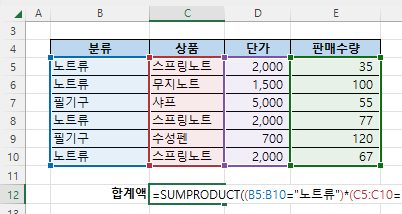
이 수식은 다음 그림과 같이 조건을 만족하는 행의 판매금액을 더해주는 방식으로 작동합니다.

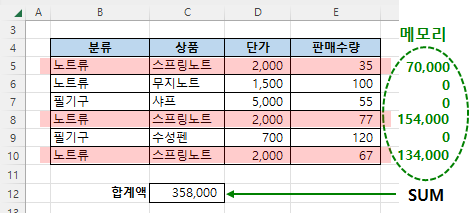
수식의 작동 원리

이 수식의 내부에서는 어떤 일이 벌어지고 있을까요?

=SUMPRODUCT((B5:B10="노트류")*(C5:C10="스프링노트"),D5:D10,E5:E10)

수식에는 3개의 인수가 들어가 있습니다.

첫번째 인수 (B5:B10="노트류")*(C5:C10="스프링노트") 는
분류가 "노트류"이고 상품이 "스프링노트" 이면 1을 반환하고 아니면 0을 반환
두번째 인수 D5:D10 은 단가
세번째 인수 E5:E10 은 판매수량

SUMPRODUCT 함수는 다음 순서대로 3개의 인수를 각 행별로 곱한 후 합계를 구하게 됩니다.

1) 최초 상태

입력된 수식의 최초 상태입니다.

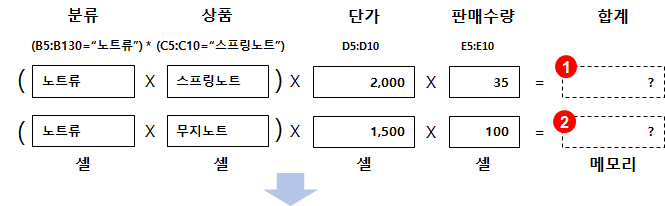
2) 조건을 만족하면 TRUE, 아니면 FALSE를 반환

두 번째 단계는 수식을 평가하여 조건을 만족하면 TRUE, 아니면 FALSE를 반환합니다.

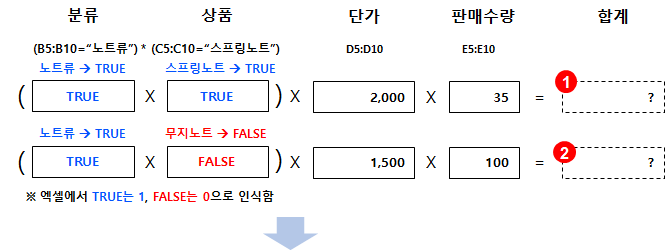
첫번째 인수 (B5:B10="노트류")*(C5:C10="스프링노트") 를 풀어보면

(B5:B10="노트류")는 B5:B10 범위에 있는 셀의 값이 '노트류'이면 TRUE, 아니면 FALSE를 반환합니다.
엑셀에서 TRUE는 1, FALSE는 0으로 인식합니다.
(C5:C10="스프링노트") 는 C5:C10 범위에 있는 셀의 값이 '스프링노트'이면 TRUE, 아니면 FALSE를 반환합니다.

3) 조건을 만족하지 못하면 0을 곱해서 계산에서 제외

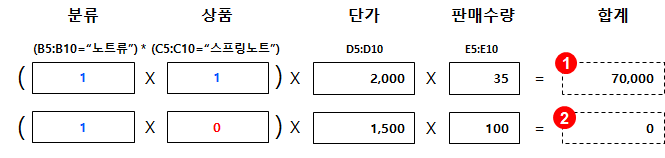
위에서 반환된 TRUE 또는 FALSE 값은 숫자 1 또는 0으로 변환됩니다.

결과적으로

0이 포함되지 않은 5행은 (첫 번째 인수 1 ) x (두 번째 인수 2,000) x (세 번째 인수 35 ) = 70,000이 됩니다.
0이 포함된 6행은 (첫 번째 인수 0) x (두 번째 인수 1,500) x (세 번째 인수 100) = 0이 됩니다.
즉 분류는 "노트류"이지만 상품명이 "스프링노트"가 아니라 "무지노트"여서 조건을 만족하지 못해 금액이 0원이 됩니다.

이렇게 행별로 구해진 값을 더하면 전체 합계 358,000원이 구해집니다.

이 수식의 핵심은 '0으로 곱한 숫자는 항상 0'이 되므로 분류가 노트류이고 상품이 스프링노트인 조건을 만족하지 못하면 0이 되도록( (B5:B10="노트류")*(C5:C10="스프링노트") → 0) 하여 SUMPRODUCT 함수로 각각의 인수를 곱해도 결과가 0이 나와서 합계에서 빠지도록 하고 조건을 만족하는 것만 합계가 계산되도록 하는 것입니다.

[ 수학 및 삼각 함수 ]

엑셀웍스 책 출간 안내

그동안 엑셀웍스에 올린 '엑셀 강좌', '함수 사용법', 여러 '실무 예제'에서 핵심만 뽑아 '된다! 엑셀 수식 & 함수' 책으로 출간하였습니다.

자세히 보기

온라인 구매처: 예스24 교보문고 알라딘